Introduction:
Any blockchain must organize the transactions in a linear order of the time of their execution, which may be different from their time of submission. Instead of trying to achieve consensus on individual transactions, it is more efficient to group them in blocks which are a finite ordered list of transactions. If a block is accepted as valid and a consensus has been achieved, that means the same thing as achieving a consensus on all of the included transactions in the mentioned order. Blocks are ordered in a sequence which is aptly named as a block-chain or simply blockchain. The chain has a beginning called the genesis block. Everyone starts off with the belief that the genesis block is valid.
The distance of any block from the genesis block in term of the number of blocks in-between is called the height of the block. The height of the genesis block can be set as zero. The height of the first block after that is one, and so on. The job of the blockchain protocol is to make sure that every honest party agrees on the block that is acceptable given any particular height.
At the heart of any blockchain, is a system that needs to agree on the system state. When multiple actors with equal privilege need to maintain a set of records, they must agree on whether some record is part of such database. This is very straightforward in a perfectly connected system with only honest parties, but it gets complicated with unreliable network and dishonest parties trying to gain from the insecurities of the system. More specifically, since honest parties cannot guarantee communication with the other honest parties and neither can they tell between honest and dishonest parties, a trivial protocol will let a dishonest party convince two different honest parties two different states of the system that cannot be true together. For example, an attacker in Bitcoin may try to make an honest party believe that he paid 1 BTC to A and make another honest party believe that he paid 1 BTC to B, where he only had 1 BTC to begin with. Such a system would allow the dishonest party to receive services from both A and B each worth 1 BTC by spending only 1 BTC altogether. In blockchain terms, such a transaction is called a double spend and a blockchain would always intend to stop such attacks. Getting multiple honest parties to agree on the correct state of the system while some dishonest parties are present is called a consensus algorithm. We will look closely into a particular kind of consensus protocol.
Bitcoin and Ethereum achieve consensus by something called a proof of work. Basically, any party can declare himself to be a leader deciding which one of the several possible correct sets of transactions is valid by solving a cryptographic puzzle ensuring some processing has been done by such party. Since there is a large reward for such a party successfully being selected as the leader, it creates a competitive environment where several parties compete to be chosen as a leader. However, since a leader is not allowed to pack conflicting/invalid transactions in the block (a block is an ordered list of valid transactions proposed by the leader), this creates only one valid chain of transactions. However, this allows some temporary disagreement between different honest parties (also known as a temporary fork), which get resolved as time goes on. It is not difficult to come by resources explaining PoW based blockchain, the reader can simply read such articles to know more unless he is already familiar with such concepts. In this blog, we dive deep into a different kind of consensus algorithm – byzantine fault tolerance or BFT.
BFT Consensus
In a BFT or a Byzantine Fault Tolerant consensus protocol, each participating party sends messages to other parties in a prescribed manner until they come to a conclusion about a certain candidate block. There is the requirement that once an honest party is able to decide a certain transaction to be valid and agreed upon, no other honest party would deny that. Each honest party confirms a consensus by making sure that a large majority of other parties (honest or dishonest) agrees to the same block for that particular height. The consensus algorithm is run fresh for each height, one after another.
The basic idea is as follows –
For every height –
- Some parties create a candidate block by compiling an ordered list of transactions. How they choose such transactions and which parties are allowed to make suggestions would be discussed later.
- After an honest party receives a set of candidate blocks, he chooses one of them – (by some mechanism that would that would not be discussed in this blog). He then lets others know about his choices by sending a signed message. We will call such a message as a P-message.
- When an honest party receives a certain number of P-messages from other parties for a particular block (among all the choices), he goes on to say that he has achieved consensus on that particular choice of a block for the current height by what is called as committing the block.
- The protocol is then repeated for the next height.
Note that each party needs to know the public key of the other parties to validate their signatures. Otherwise, one single dishonest party can send the P-messages on behalf of everyone to create a consensus of his choice.
The system cannot of course work with an arbitrary number of dishonest parties, there must be a limit for the maximum number of dishonest parties the system can be protected against. In the following section, we will discuss this limit.
Maximum number of dishonest users for achieving consensus
Before we get to limits, we need to state the conditions the protocol needs to satisfy:
- Safety: Whenever any honest user commits a block for a given height, no other honest user can commit a different block at the same height even when the attacker has full control of the network. This ensures that the commits are final and unchangeable. So once a transaction is included in a block committed by any honest user, he knows for sure that that transaction cannot be undone. Note that only the honest party himself can know that since any other party cannot know whether he is honest or not and a dishonest party can do anything including committing something for no good reason. The protocol needs to ensure this property even when the attacker has full control of the network and can create an arbitrary number of network partitions.
- Liveness: It should always be possible to commit a new block by all honest parties at the next height as long the network connection works, i.e. the attacker loses control of the network. Basically, this condition is about not getting into a deadlock. This is important for the chain to proceed. Of course, the parties cannot commit if the network does not forward their P messages, so this has to only work when the network is connected.
That being said, we try to figure out the maximum number of dishonest user any system can support to achieve consensus. Let us assume that any honest user needs to see P messages for the same block for the given height from a t fraction of the total number of parties. That is if there are a total of N parties, the honest users would look for more than t/N P messages supporting the same block before they commit the block. Let us also assume that z is the maximum fraction of dishonest parties that the protocol can support.
We first see what is required to achieve condition 1. We already assumed that the attacker has full control of the network. We also assume that the dishonest parties make a coalition among themselves to form a combined attacker. The aim of the attacker is to make two different honest users commit two different blocks. The attacker partitions the network into three groups. One containing x/N honest users (we will call this partition A), one containing the rest of the honest users (partition B) and the last partition containing all the dishonest parties (partition C). This means the fraction of parties in partition B is (1-x-z). Note that the attacker can control the network and all delivery of messages, but cannot create a P message on behalf of an honest user. Now the attacker tries to make both of those partitions commit different blocks for the same height.
Since the attacker can have z fraction of P messages for both blocks, the total fraction of P messages the attacker can achieve for a block in partition A is x+z. Similarly, the total fraction of P messages the attacker can create in partition B is z+(1-x-z) = 1-x. Since any BFT protocol needs to make sure that conflicting blocks cannot be committed, at least one of them must be less than or equal to t.
Since the attacker can choose any value for x, it must be so that for any value of x either x+z ≤ t or 1-x ≤ t.
The reader can now note that the logical condition (A or B) to be true means either A has to be true or B has to be true. This means if A is false, then B must be true. This is the same thing as (not A) ⟹ B.
So, for all x, (x+z ≤ t or 1-x ≤ t) is the same thing as saying for all x, x+z > t ⟹ 1-x ≤ t.
This can be simplified as x+z > t ⟹ x+z ≥ 1-t+z (1) .
When stated this way we can see that this condition would be met if t ≥ 1-t+z or 2t -1≥ z or z ≤ 2t-1 (2).
That would get what we want. But we have to prove that this condition is really necessary.
Suppose it is not true that z ≤ 2t-1; so, it must be true that z> 2t-1.
We will create a condition where x+z > t but x+z < 1-t+z thus violating (1). The minimum possible value for x+z is of course z and maximum is 1. The attacker can choose any value for x such that x+z is in that range. Suppose, m = max(z, t) and the attacker chooses x = (m + 1-t+z)/2 -z so that x + z = (m + 1-t+z)/2 .
We have assumed that z > 2t-1 , so 1-2t + z > 0 or 1-t+z > t > 0 (3) . Hence, since m = max(z, t), x + z = (m + 1-t+z)/2 > z. This means such an x is admissible.
Also, 1-t+z > t (according to 3) and since t<1 (as it a fraction), 1-t+z > z (4). (3) and (4) together implies 1-t+z > max(z, t) =m or m < 1-t+z (5). Hence, x + z = (m + 1-t+z)/2 < ((1-t+z) + 1-t+z)/2 = 1-t+z.
Basically, since x + z is the mean of 1-t+z and m, and since 1-t+z > m, it must be that m < x+z < 1-t+z . Observe that m=max(z,t) we have t ≤ m < x+z < 1-t+z which achieves the contradiction. Hence, we have proved that it has to be the case that z ≤ 2t-1 according to (2).
Now, let us consider condition 2. It simply says that when the network is connected, the commit must be possible. So, the fraction of honest parties must be able to cause a commit. This means (x+(1-z-x)) = 1-z > t or z < 1-t . The following diagram shows the allowable values for z.
The fraction of dishonest user is marked in green. The maximum possible value for z is of course just below the intersection of the lines z = 1-t and z = 2t-1. We say ‘just below’ and not on the intersection because z < 1-t and so z cannot be on this line. If the intersection is at t=t0, we have 1-t0 = 2t0 -1 or 3t0 = 2 or t0 = ⅔ . Hence, z < 1-t0 = 1-⅔ = ⅓ . Hence the maximum fraction of dishonest users have to be less than ⅓ and that would be achieved when t= ⅔. So if there are f dishonest parties in the system, there must be at least 2f+1 honest parties, so that the total number of parties is 3f+1 which makes the number of dishonest parties strictly less
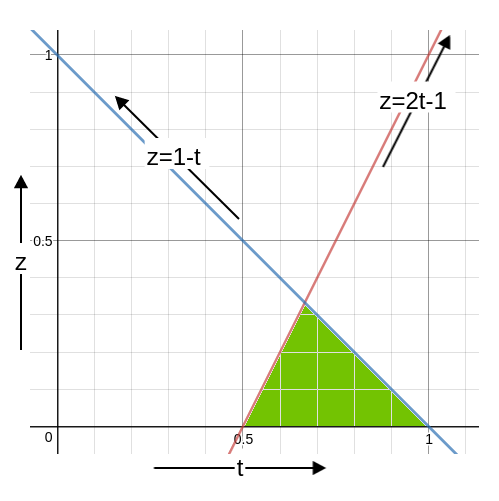
than the ⅓ fraction of the total number of parties. This also means the threshold here is floor(⅔(3f+1)) which is 2f+1 We will count the users in terms of f from now on.
Summary: The red line in the above graph is the safety line. The z below that can maintain the safety of the chain. The blue line is the liveness line. The z below that can maintain liveness of the chain. Since both must be maintained, only the green area is allowed for the value of z. The maximum value of z is, of course, the apex which is reached when z = ⅓. In fact, z must be less than ⅓ for reasons described earlier.










